Bài toán cầu hôn và giải pháp cho Bộ Giáo dục

Tại ngày hội “Một ngày với Toán học” diễn ra tại Viện Toán học hôm 10/10, GS. Hà Huy Khoái đã có bài giảng “Toán học với thị trường, tuyển sinh và gả chồng dựng vợ” trước đông đảo người yêu toán. 

Bài toán gả chồng dựng vợ mà ông còn gọi là “bài toán cầu hôn” chính là thuật toán “chấp nhận trì hoãn” của Gale Shapley mà ứng dụng của GS. Alvin Roth vào lĩnh vực kinh tế đã giành giải Nobel Kinh tế năm 2012.

Thuật toán Gale Shapley được GS. Hà Huy Khoái giải thích bằng bài toán cầu hôn như sau: Có 4 chàng trai là Adam, Bob, Charlie, Don và 3 cô gái là Mary, Jane và Kate. 4 chàng trai có cảm tình với 3 cô gái theo một thứ tự ưu tiên nhất định và ngược lại 3 cô gái cũng có cảm tình với 4 chàng trai theo một thứ tự ưu tiên khác.

Và thuật toán G. Shapley sẽ giải quyết vấn đề này bằng cách đưa ra phương án tốt nhất cho 4 chàng trai (hoặc 3 cô gái) dựa trên thứ tự ưu tiên của họ.

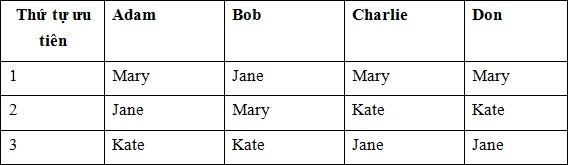
Giả sử thứ tự ưu tiên của 4 chàng trai như sau:

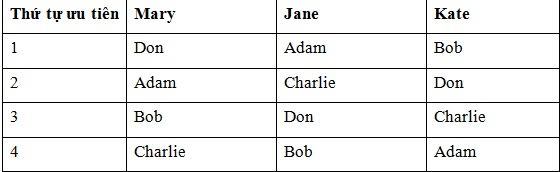
Giả sử thứ tự ưu tiên của 3 cô gái như sau:

Giả sử bài toán này sẽ ưu tiên quyền lợi của 4 chàng trai trước, nghĩa là để các chàng trai đưa ra lựa chọn của mình trước (nếu dựa trên ưu tiên quyền lợi của các cô gái, kết quả sẽ khác đôi chút).

Ngày đầu tiên, 4 chàng trai đi cầu hôn ưu tiên số 1 của mình, nghĩa là Bob cầu hôn Jane, và cả 3 chàng trai Adam, Charlie và Don đều cầu hôn Mary.

Mary vì có tới 3 sự lựa chọn nên sẽ chọn ưu tiên tốt nhất của mình trong số 3 chàng trai, đó là Don (ưu tiên số 1 của Mary).

Jane vì chỉ có Bob cầu hôn nên sẽ chọn Bob tạm thời (chấp nhận tạm thời). Kate chưa có ai cầu hôn trong ngày đầu tiên.

Sang ngày thứ hai, vì Mary đã chọn Don nên Adam và Charlie đi cầu hôn ưu tiên số 2 của mình. Adam cầu hôn Jane và Charlie cầu hôn Kate. Vì ưu tiên số 1 của Jane là Adam nên Jane chấp nhận Adam, loại Bob. Kate chỉ có duy nhất Charlie cầu hôn nên tạm thời chấp nhận Charlie.

Ngày thứ ba, chỉ còn Bob chưa được ai chấp nhận, Bob cầu hôn Kate. Bob là ưu tiên số 1 của Kate, trong khi Charlie là ưu tiên số 3 nên Kate chọn Bob, loại Charlie.

Như vậy, theo cách nói vui của GS. Hà Huy Khoái, cuối cùng Charlie “ế vợ”.

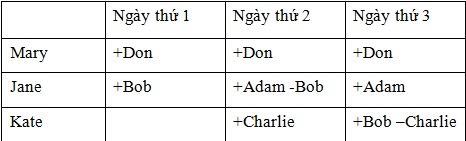
Quá trình “cầu hôn” và “chọn lựa” này có thể được biểu diễn bằng bảng sau:

Bài toán cầu hôn không có thực trong cuộc sống thực tiễn nhưng cách giải quyết vấn đề của thuật toán này có thể áp dụng ở nhiều lĩnh vực. Theo GS. Hà Huy Khoái, giai đoạn 1945-1951, thị trường tuyển dụng bác sĩ ở Mỹ bùng nổ do nhu cầu bác sĩ ở các bệnh viện quá lớn. Hậu quả của việc các bác sĩ tự ứng tuyển và các bệnh viện tự chọn lọc theo nhu cầu của riêng mình là các bệnh viện đưa ra thời hạn chấp nhận gấp, sinh viên y khoa nhận chỗ làm quá sớm… Vì thế, Chính phủ Mỹ đã thành lập một trung tâm điều phối có tên là National Resident Matching Program (NRMP) để tiếp nhận tất cả nguyện vọng của các bác sĩ cũng như các bệnh viện, từ đó điều phối sao cho phù hợp nhất. Năm 1984, nhà kinh tế Alvin Roth phát hiện ra thuật toán của NRMP áp dụng gần với thuật toán “chấp nhận trì hoãn” của Gale Shapley.

Trước năm 2004, quá trình tuyển sinh vào các trường công ở New York áp dụng lý thuyết “chấp nhận tức khắc” cũng dẫn tới tình trạng học sinh không đăng ký nguyện vọng thật của mình. Do đó, cần có một phương án giải quyết những vấn đề trên nhằm đảm bảo tính ổn định cũng như khuyến khích sự thành thật trong việc đăng ký nguyện vọng.

GS. Hà Huy Khoái khẳng định, Bộ Giáo dục có thể áp dụng kết quả của thuật toán này vào công tác xét tuyển nguyện vọng đại học, cao đẳng để tránh tình trạng rút ra rút vào hồ sơ, gây mệt mỏi cho thí sinh như mùa tuyển sinh vừa qua.

Giống như bài toán cầu hôn, vẫn là quá trình rút ra rút vào nhưng tất cả được thực hiện bởi máy móc, phần mềm. Việc của các thí sinh là đưa ra danh sách thứ tự ưu tiên của mình, các trường cũng đưa ra thứ tự ưu tiên của mình: điểm thi, học bạ, hạnh kiểm… Với các trường đặc thù có thể là chiều cao, cân nặng, năng khiếu… Sau đó máy móc sẽ thực hiện toàn bộ quá trình rút ra rút vào đó và đưa ra một kết quả tốt nhất cho các thí sinh, đảm bảo rằng sẽ không có thí sinh nào điểm thấp hơn mình vào được trường đó mà mình không vào được.

Theo GS. Hà Huy Khoái, đây là giải pháp duy nhất cho vấn đề tuyển sinh hiện nay. Giải pháp này đảm bảo các yếu tố: cho phép các trường đề ra thứ tự ưu tiên cho mình, đảm bảo quyền lợi của học sinh: nêu nguyện vọng thật, học sinh được theo học tại trường ưu tiên cao nhất có thể theo thứ tự ưu tiên tùy thuộc kết quả của thí sinh, loại bỏ được yếu tố “ảo” và tiết kiệm chi phí.

“Chúng tôi đã thử nghiệm và cho kết quả tốt. Chỉ trong vòng 2 tiếng xứ lý được dữ liệu của 1 triệu thí sinh. Làm tất cả chỉ trong vòng 1 ngày là xong” – GS. Hà Huy Khoái khẳng định.

Ông cũng cho biết Cục Khảo thí cũng tỏ ra rất tâm đắc với phương án này và có mời ông tới nói chuyện với các trường. “Các trường tốp đầu hiểu rất nhanh và thích phương án này nhưng không hiểu sao lãnh đạo nhiều trường khác thì không muốn áp dụng. Họ bảo cứ để họ tự làm theo cách truyền thống” – ông nói.

“Tôi cũng rất tiếc vì năm vừa rồi Bộ không áp dụng. Có lẽ Bộ còn lo ngại các trường”.

GS. Hà Huy Khoái cũng cho rằng cái khó trong vấn đề này không phải là vấn đề kỹ thuật mặc dù để áp dụng vào tuyển sinh cần phải cải tiến đôi chút, mà khó nhất là thuyết phục được xã hội, làm thế nào để các phụ huynh, các em học sinh, các trường hiểu được và đồng tình. Ban đầu, giải pháp NRMP ở Mỹ cũng không phải bác sĩ nào cũng tham gia nhưng sau đó họ nhận ra không tham gia thì bị thiệt.

Ông cũng cho biết các nhà khoa học cũng đã gợi ý Bộ trước mắt dùng 80% chỉ tiêu để áp dụng thuật toán này. “ Tôi rất hy vọng năm sau Bộ sẽ áp dụng. Theo tôi đây là giải pháp duy nhất” – ông nói.

Nguyễn Thảo - VNN

 Xem thêm Bài toán hôn nhân bền vững

Read More

Lý giải đằng sau những bài toán tính gà kiểu Mỹ

Những bài toán đơn giản nhưng có lời giải khó hiểu và phức tạp thậm chí với cả người lớn gần đây được chia sẻ nhiều trên các phương tiện truyền thông của Mỹ. Đây được cho là những bài toán được giải theo quy định trong bộ Sáng kiến Tiêu chuẩn chung liên bang – Common Core State Standards Initiative (gọi tắt là Common Core).

Phụ huynh Mỹ lúng túng

Chị Jennifer Craig nhìn chằm chằm vào bài tập toán của cô con gái. Đó là một phép nhân 3 chữ số khá đơn giản. Nhưng cô con gái 10 tuổi của chị giải nó bằng cách vẽ biểu đồ, tách số, nhân, cộng và một số bước rắc rối khác.

“Tôi thấy điên đầu” – bà mẹ 31 tuổi nói.

Và đó là lý do tại sao chị có mặt trong lớp học của con gái vào tối thứ Hai, cùng với nhiều phụ huynh khác, ngồi trên những chiếc ghế trẻ con, nghe cô giáo Alyshia Thomas giảng giải về cách làm toán mới.

Hầu hết học sinh ở các trường công của Mỹ đều đang học Toán rất khác với thời của bố mẹ chúng do sự xuất hiện của Common Core.

Những thay đổi này khiến nhiều phụ huynh lúng túng khi giúp con làm bài tập về nhà, đặc biệt là những người có con học tiểu học.

Melissa Palermo là một giáo viên lớp 4 tràn đầy nhiệt huyết. Cô là người tập huấn cho các giáo viên khác cách giải Toán mới ở Trường Nathaniel Hawthorne. “Phần khó khăn nhất là bài tập về nhà bởi vì nó rất khó với các bậc phụ huynh. Nhiều phụ huynh nghi ngờ chính mình vì họ chưa từng nhìn thấy những cách giải như thế này trước đây”.

“Họ thất vọng vì không thể giúp được con mình” – Bill Hanlon, một giáo viên dạy Toán ở Las Vegas cho hay. “Một trong những thông điệp mà tôi muốn gửi tới các giáo viên là nếu bạn giao những bài tập về nhà mà phụ huynh chưa từng thấy trước đây, hãy gửi kèm một mẩu giấy giải thích việc mà chúng ta đang làm, tại sao chúng ta lại làm vậy đồng thời đưa ra vài ví dụ. Nếu không, bạn sẽ nhận được rất nhiều thắc mắc”.

Cô Diane Dunaskiss – hiệu trưởng Trường Tiểu học Pine Tree khẳng định: “Phương pháp làm toán mới khuyến khích học sinh nghĩ sâu hơn. Khi bạn hiểu mình đang học cái gì, bạn sẽ ứng dụng nó vào việc bạn đang làm trong cuộc sống thực”.

Trước đây, Toán được học theo kiểu ghi nhớ một loạt các công thức, số liệu, mẹo vặt. Các chuyên gia cho rằng hậu quả của cách học này là học sinh Mỹ phải vật lộn với môn Toán. Gần 2/3 học sinh từ lớp 4 đến lớp 8 không đạt trong các bài kiểm tra Toán quốc gia. Phương pháp Common Core khác với phương pháp cũ ở chỗ tập trung vào bản chất đằng sau các hoạt động Toán học và nhấn mạnh vào việc có nhiều cách để đưa ra cùng một câu trả lời.

Common Core kỳ vọng học sinh sẽ không chỉ tìm được đáp án mà còn giải thích được tại sao.

Tại sao cần Common Core?

Bộ tiêu chuẩn giáo dục liên bang đã có từ đầu những năm 90.

Nhưng đến đầu những năm 2000, mỗi bang lại phát triển và áp dụng những tiêu chuẩn học tập riêng của mình.

Lúc này mỗi bang đều có những khái niệm riêng về “đủ điều kiện”. Việc thiếu một chuẩn hóa chung cộng với thực tế thành tích của học sinh Mỹ khá khiêm tốn so với các quốc gia khác trên các bảng xếp hạng quốc tế là lý do tại sao các bang quyết định phát triển Common Core vào năm 2009.

Common Core là tập hợp các tiêu chuẩn học thuật cao ở môn Toán và Đọc hiểu. Common Core được tạo ra để đảm bảo rằng tất cả học sinh tốt nghiệp phổ thông đều có đủ kỹ năng và kiến thức cần thiết để học tốt ở đại học, để làm một công việc nào đó và để bước vào cuộc sống, bất kể các em sống ở đâu.

Bộ tiêu chuẩn này được soạn thảo bởi các chuyên gia và giáo viên trên khắp nước Mỹ. Những tiêu chuẩn này cũng là cách để giáo viên đo lường sự tiến bộ của học sinh trong suốt năm học và để đảm bảo rằng các em đang đi đúng hướng để đạt được thành công trên con đường học tập.

Tranh cãi vẫn chưa dứt

Bất chấp việc Common Core được áp dụng nhanh chóng và rộng rãi, nhóm chỉ trích vẫn phản ứng dữ dội. Một số phụ huynh đăng tải những bài toán và lời giải theo kiểu Common Core bằng giọng điệu mỉa mai, châm biếm. 

Read More

Bài toán lớp 7 khiến phụ huynh, học sinh thắc mắc

Bạn Nguyễn Thanh Như gửi đến VnExpress bài toán trong đề kiểm tra lớp 7 của con với các cách giải khác nhau.

Cách giải một là của con chị Như và một số học sinh trong lớp; cách hai của phụ huynh học sinh; cách ba của cô giáo; còn cách thứ tư là phương pháp giải của sách giáo khoa cũng như đa số sách tham khảo toán 7. 

Dưới đây là bài viết theo tinh thần của độc giả Nguyễn Thanh Như. 

Theo bạn trong 4 cách giải trên, cách nào đúng, cách nào sai và vì sao?

Qua bài viết "Bài toán lớp 7 khiến phụ huynh, học sinh thắc mắc" tôi thấy rất nhiều người quan tâm và comment trái chiều. Tôi cũng thấy hào hứng, xin góp bài viết nêu ra quan điểm của mình.

Về các lời giải thì trò sai trong việc chuyển vế, cô giáo sai vì hiểu sai khi đơn giản biểu thức, phụ huynh và sách giáo khoa giải đúng.

Vấn đề mấu chốt của bài toán chính là việc biểu thức 1/2 : 2x đơn giản thành x/4 hay là 1/4x?

Quan điểm tôi là 1/2 : 2x phải hiểu là 1/4x chứ không phải là x/4 vì:

Thứ nhất: Khi viết 2x có nghĩa tương đương 2*x, tuy nhiên nó còn có nghĩa là x phụ thuộc hoàn toàn vào số 2 trước nó. Tùy vai trò của số 2 trong biểu thức mà x phải đi theo và có ý nghĩ trong biểu thức. Như trong bài toán số 2 là số chia của phân số 1/2 nên 2x cũng phải là số chia của 1/2 luôn.

Thứ hai: Ngoài ra phép nhân có tính giao hoán 2x hay 2*x = x*2, vì vậy 1/2 : 2x có thể viết lại.

1/2 : x*2 hay 1/2 : x2.

Nếu "cụm" 2x này không hiểu nhất quán lúc này 1/2 : 2*x và 1/2 : x*2 lại khác nhau?! Vậy thì cứ quan điểm như phía trên dù có viết 1/2 : x*2 hay 1/2 : 2*x vẫn đơn giản lại là 1/4x.

Thứ ba: Về cách ra đề đối với học sinh đã học qua phân số thì nên thay các dấu tường minh "x - nhân", ": - chia" thành "." hay "/", các dấu tường minh này chỉ còn phù hợp cho học sinh cấp 1.

Khi ra đề nên tối giản, đưa đúng mục tiêu và trọng tâm yêu cầu đến học sinh, không nên để ghép các phép tính dễ gây hiểu nhằm, nhất là trong các phương trình. Ví dụ phương trình ax2 - b = 0 thì không cần triển khai từ số hằng a hay b hay một biểu thức loằng ngoằng bằng các phép tính + - x : của cấp 1.

Thứ tư: Các ý kiến của bạn đọc dùng kết quả thế vào để biết đúng sai thì cũng vô ích khi không thống nhất 1/2 : 2x là x/4 hay là 1/4x. Các máy tính điện tử đầu vào cũng phải theo quan điểm (1) thì mới cho kết quả đúng.

Tôi là kỹ sư phần mềm, từng học chuyên toán Amsterdam (Hà Nội) và đã được trải qua cả nền giáo dục trong, ngoài nước. Thực chất bài toán lớp 7 không phải về vấn đề toán học mà là vấn đề thống nhất quy chuẩn. Nếu không thống nhất được thì dĩ nhiên sẽ ra những kết quả khác nhau. Mọi người nhầm tưởng toán học luôn thống nhất, nhưng thực ra toán học từ xưa nay vẫn luôn tồn tại những kết quả khác nhau trong những trường hợp khác nhau. Lấy ví dụ mọi người luôn được dạy x/0 không được định nghĩa, nhưng thực tế trong một số cấu trúc toán học, vẫn có thể định nghĩa được. Hoặc phép toán 1+2+3+... = -1/12 nghe có vẻ vô lý nhưng lại rất quan trọng trong lý thuyết dây (string theory). Trở lại bài toán lớp 7 này, vấn đề cơ bản gây hiểu nhầm là 1/2:2x nên được hiểu là (1/2:2)x=(1/4)x hay 1/2:(2x)=1/(4x). Trong một số nền toán học từ trước đến nay, ax luôn được ưu tiên (implied multiplication) với a được gọi là hệ số của x. Tuy nhiên, điều này dễ gây hiểu nhầm nên toán học hiện đại hầu như đã bỏ sự ưu tiên này và chỉ tuân theo quy tắc trái sang phải cho nhân chia. Điển hình như engine toán học lớn Wolfram Alpha đã bỏ implied multiplication từ năm 2013. Các bạn có thể thử 1/2x vào Wolfram Alpha sẽ cho kết quả x/2. Vấn đề thứ hai là dấu ":". Ở Việt Nam và một số nền toán học không dùng tiếng Anh thì ":" được hiểu là phép chia. Tuy nhiên thực tế là ":" được sử dụng làm tỷ lệ trong toán học hiện đại. Ví dụ 2:1:3 được hiểu là tỷ lệ giữa cam táo nho chẳng hạn, chứ không phải phép chia kết quả 2/1/3=2/3. Tỷ lệ này phải được giữ nguyên ví dụ 2x:3y là một tỷ lệ và khác với 2x/3y. Ở đây bài toán nhiều khả năng dùng ":" cho phép chia chứ không phải tỷ lệ. Nên được viết lại thành (1/2)/2x=-1/3 tức (1/4)x=-(1/3) tức x=-(4/3).

Độc giả Nguyễn Chiến Thắng chia sẻ cách nhìn của anh sau bài toán lớp 7 gây tranh cãi.

 

 

 

 

 

 

 

 

 Nguồn: Vnexpress [1],[2],[3],[4]

Read More

Nỗi xấu hổ của thế hệ trẻ?

 Mùa xuân về, chúng ta hay nói đến tuổi trẻ, đến hiền tài là nguyên khí quốc gia. Mùa xuân này, có ai thấy “nhục”, thấy cay mũi khi Việt Nam bị đánh giá là quốc gia “thiểu năng trí tuệ”.

“Lĩnh vực giáo dục đào tạo, khoa học công nghệ phát triển chậm chạp, lạc hậu so với các quốc gia trong khu vực. Nền sản xuất trong nước ít tạo ra được các sản phẩm có giá trị gia tăng cao, tham gia vào chuỗi các giá trị toàn cầu. Tổ chức Sở hữu trí tuệ Thế giới thuộc Liên hiệp quốc công bố bảng xếp hạng chỉ số đổi mới toàn cầu năm 2012, trong đó Việt Nam bị tụt hạng, và theo kết quả những năm gần đây, Việt Nam nằm dưới lằn ranh trung bình. Các chuyên gia trong nước vào ngoài nước cảnh báo nếu không có sự đột phá trong sáng tạo, đổi mới thù Việt Nam sẽ là một quốc gia thiểu năng trí tuệ”, đó là một đoạn trong bài xã luận “Nhân tài và thế nước” đăng trên báo Lao động số Tết.

Trong chương trình kinh tế trên VTV chiếu vào dịp Tết, một so sánh được chỉ ra: lợi nhuận bán 3 tấn gạo của Việt Nam mới đúng bằng lợi nhuận bán 1 chiếc iPhone 5 của Apple. Tức là cùng một giá trị lợi nhuận của sản phẩm, nhưng con số khối lượng sản phẩm thì chúng ta phải gấp họ tới 27.000 lần. 3 tấn gạo, là biết bao mồ hôi công sức của bao người nông dân, nhưng 1 sản phẩm iPhone 5, thì ở đó bao gồm bao nhiêu hàm lượng trí tuệ? So sáng không phải để làm giảm giá trị của sản xuất nông nghiệp, nhưng thực tế chỉ ra, nếu không có hàm lượng trí tuệ cao, thì chúng ta phải đổi lại bằng công sức lao động tay chân.

Phải bán đến cả vài tấn gạo mới thu được lợi nhuận bằng bán 1 chiếc iPhone 5. Nếu không có hàm lượng trí tuệ cao trong sản phẩm, thì chúng ta phải đổi lại bằng mồ hôi công sức lao động tay chân.

Khoa học của chúng ta phát triển chậm chạp, lạc hậu hơn so với các quốc gia trong khu vực, cái đó chẳng cần những con số thống kê làm gì, cứ đặt chân sang nước khác là ta nhìn rõ ngay những cái ta kém họ. Singapore, Thái Lan, Malaysia, về tài nguyên, họ đâu có gì hơn chúng ta, nhưng họ phát triển hơn ta ở nhiều cái, nhiều lĩnh vực. Rồi năm qua, có 1 số liệu thống kê nào đó chỉ ra, Việt Nam có rất ít những bằng sáng chế khoa học, rồi thì các công trình khoa học có ứng dụng vào thực tế, thúc đẩy sản xuất và có ý nghĩa nhân văn, cũng không nhiều.

Thanh niên, có ai cảm thấy nhục, thấy xấu hổ, trước những vấn đề trên hay không? Có ai xấu hổ, tự ái, khi Việt Nam, nếu không nỗ lực, thì sẽ trở thành một quốc gia thiểu năng trí tuệ hay không?

Con người Việt Nam không ngu si, thanh niên Việt Nam không dốt nát, cái đó là truyền thống dân tộc, là trí tuệ cha ông truyền lại, trí tuệ và lòng quả cảm của dân tộc Việt, là điều cả thế giới phải công  nhận?

Chúng ta không thiếu người tài, người giỏi, chúng ta không thiếu trí tuệ. Vậy tại sao, Việt Nam vẫn là nước kém về khoa học công nghệ? Do đâu, và ai là người giải quyết?

Không ai khác ngoài thế hệ trẻ, thế hệ đứng trước sứ mệnh lịch sử phát triển đất nước, khi được kế thừa lại thành quả bằng mồ hôi xương máu cha ông, một thế hệ những 7x,8x, 9x sướng hơn nhiều so với cha anh đi trước, sống trong hòa bình, thoải mái hơn về vật chất và đầy đủ phương tiện để bước ra thế giới hay tự sống khỏe trên quê hương mình.

Phát điên phát cuồng quá đáng, sống tự kỉ quì gối vì những cái không đáng có. Có thể trông đợi gì ở những thanh niên kém bản lĩnh sống như thế này?

Bao nhiêu vụ tai nạn giao thông chết người trong cái Tết này là do thanh niên uống rượu rồi phóng nhanh vượt ẩu? Ai đó gọi thế hệ thanh niên ở nông thôn giờ đây là thế hệ “lên nóc nhà rồi bắt con gà”, cứ nhạc vào là “bay lắc” tùm lum, phóng xe bạt mạng "đường làng là của ta". Ai đó gọi thanh niên đô thị là một thế hệ tự kỉ, suốt ngày lên facebook chém gió, than thở kêu chán rồi chửi đời. Còn “cái bọn trẻ sắp lớn” thì là những đứa trẻ hóa rồ vì các Ồ-pa Hàn Quốc, hời hợt và quên mất thậm chí quay lưng lại với các giá trị truyền thống. Đánh giá như thế là quá phiến diện, thiếu tích cực, chỉ nhìn mặt tiêu cực, nhưng nhìn lại thử xem, chẳng phải rất nhiều “thanh niên thế hệ mới” đang sống như vậy sao.

Anh diễn viên hài Quang Thắng vừa rồi đóng Táo kinh tế đã nhảy “hoang mang xì-tai” rồi hát “một năm kinh tế buồn”. Sẽ còn nhiều khó khăn trong năm Qúy Tỵ, kinh tế vẫn có nguy cơ “buồn” hơn, sẽ còn nhiều những hệ quả nếu chúng ta không sáng tạo, và vượt khó vươn lên.

Tin rằng, những bí thư chi bộ xã, nhưng doanh nhân thành đạt, những nhà khoa học tài giỏi, nhà báo, nhà văn, bác sĩ, chiến sĩ trên địa đầu Tổ quốc…những con người đáng vinh danh trong thời kì phát triển mới của Đất nước, sẽ từ những người trẻ biết nhìn xa trông rộng, biết sống có lý tưởng, nhìn xa hơn những hoài bão cá nhân, là những người trẻ, biết thấy xấu hổ, thấy nhục của ngày hôm nay.

“Hiền tài là nguyên khí của quốc gia, nguyên khí thịnh thì thế nước mạnh mà hưng thịnh, nguyên khí suy thì thế nước yếu mà thấp hèn”. Trong những ngày đầu xuân, khi chúng ta cùng tưởng nhớ cua Quang Trung thắng giặc ngoại xâm, thì cũng hãy nhìn về phía trước, đặt niềm tin hơn vào thế hệ trẻ, và cũng mong thế hệ trẻ, hãy sống sao cho có ý nghĩa hơn.

Tên bài gốc "Chiếc iphone 5 giá hơn tấn gạo và nỗi xấu hổ của thế hệ trẻ?"

Theo Vnmedia

Read More

Vẻ đẹp của người đứng một mình

“Mọi vấn đề của con người xuất phát từ chỗ họ không thể ngồi yên một mình trong phòng” - nhà toán học và triết học Pháp Blaise Pascal đã nói vậy vào giữa thế kỷ 17. 

Ảnh: mufonohio.com

Căn nguyên của các rắc rối, theo ông, là chúng ta luôn tìm cách chạy trốn bản thân. Không muốn đối diện với chính mình, tâm trí con người luôn lùng sục điều kích thích tiếp theo, như một con khỉ không thể ngừng văng mình tới cành cây trước mặt. Từ cãi vã với hàng xóm tới xung đột giữa các quốc gia, nhiều điều tệ hại bắt nguồn từ lý do này.

Đọc tiếp »

Read More

Thuật toán Euclid tìm ƯCLN

Giải thuật Euclid, hay thuật toán 
Euclid, là một giải thuật giúp tính ước số chung lớn nhất (ƯSCLN) của hai số 
một cách hiệu quả. Giải thuật này đã được biết đến từ khoảng năm 300 trước Công 
Nguyên. Nhà toán học Hy Lạp cổ Euclid đã viết giải thuật này trong cuốn sách 
toán nổi tiếng Elements.

Ở dạng đơn giản nhất, thuật toán Euclid bắt đầu với cặp 
số nguyên dương, và tạo ra một cặp số nguyên dương mới bao gồm số nhỏ hơn và 
phần dư của của phép chia hai số ban đầu. Quá trình được tiếp tục cho đến khi 
hai số trong cặp bằng nhau, giá trị lúc đó sẽ trở thành ước số chung lớn nhất 
của cặp số ban đầu.

Hình 
minh họa thuật toán Euclid để tìm ước số chung lớn nhất 
(ƯSCLN) của hai đoạn thẳng BA và DC, độ dài của cả hai đều là bội số của một đơn 
vị độ dài chung. Vì độ dài của DC ngắn hơn nên nó được dùng để đo cho BA, nhưng 
việc này chỉ làm được một lần do phần còn lại là đoạn EA ngắn hơn DC. Bây giờ EA 
lại được dùng để đo độ dài đoạn DC hai lần. Cuối cùng đoạn FC được dùng để đo độ 
dài đoạn EA ba lần. Vì không còn đoạn nào dư ra nên quá trình này kết thúc với 
FC trở thành ƯSCLN. Phía bên phải là ví dụ của Nicomachus với hai số 49 và 21 có 
kết quả ƯSCLN là 7.

Nguyên lí chính của thuật toán là ước số chung lớn nhất 
của một cặp số không thay đổi với hiệu của hai số đó. Ví dụ như ƯSCLN của 252 và 
105 chính bằng ƯSCLN của 147 (= 252 − 105) và 105. Vì số lớn hơn trong cặp số bị 
giảm giá trị nên việc lặp đi lặp lại thuật toán này giúp tạo ra những số ngày 
càng nhỏ và đến một lúc nào đó quá trình này sẽ kết thúc — khi cặp số còn lại 
hai số bằng nhau (nếu quá trình được thực hiện thêm một bước nữa, sẽ có một 
trong hai số trở thành số 0).



Bổ đề: 

Giả 
sử a = bq + r, với a, b, q, 
r là các số nguyên, ta có:



Trong 
đó r = a mod b

Ví dụ:

Tính 
ước số chung lớn nhất của 91 và 287.

Trước 
hết lấy 287 (số lớn hơn trong 2 số) chia cho 91:


287 = 91*3 
+ 14 (91 & 14 sẽ được dùng cho vòng lặp 
kế)

Nhận xét: bất kỳ số nào chia hết bởi 287 và 91 cũng sẽ 
chia hết bởi 287 - 91*3 = 14. Tương tự, số chia hết bởi 91 và 14 cũng chia hết 
bởi 91*3 + 14 = 287. Do đó, ƯSCLN(91,287) = ƯSCLN(91,14). Bài toán trở thành tìm 
ƯSCLN(91,14). Lặp lại quy trình trên cho đến khi phép chia không còn số dư như 
sau:


91 = 14*6 
+ 7 (14 & 7 sẽ được dùng cho vòng lặp 
kế)

14 = 7*2 (không còn số dư, kết thúc, 
nhận 7 làm kết quả)

Cuối 
cùng ta có: 7 = ƯSCLN(7,0) = ƯSCLN(14,7) = ƯSCLN(91,14) = ƯSCLN(287,91).



Chương trình 
Scilab:
disp("+---+---+---+---+---+---+---+---+---+---+---+")
disp("     TÌM ƯCLN CỦA HAI SỐ")                    // Theo thuật toán Euclide
disp("                             ")
//
clear

// Hàm tìm số dư của x chia y
function d=sodu(x, y)
    d=x-floor(x/y)*y
endfunction

// Hàm tìm UCLN
function u=ucln(x, y)
        while y>0 
        t=sodu(x,y)
        x=y
        y=t
        end
    u=x             // x là ƯCLN cần tìm
    endfunction

a=input("Nhập số thứ nhất: ")
b=input("Nhập số thứ hai: ")
disp(ucln(a,b))
 

Tham khảo Giải thuật Euclid - Wikipedia

Read More

Phần mềm Scilab: Tính toán khoa học và lập trình

“Scilab is the closest that you can get to Matlab without spending a penny”

 

Scilab là gói phần mềm tính toán số phát triển từ năm 1990 bởi các nhà nghiên cứu từ INRIA và École nationale des ponts et chaussées (ENPC). Tạo ra vào tháng 5 năm 2003, nó được phát triển và duy trì bởi INRIA.
Scilab là phần mềm nguồn mở cho việc tính toán khoa học ở mức cao tương tự như Matlab, Octave, Rlab trên nhiều lĩnh vực: giải phương trình vi phân/tuyến tính, xử lý tín hiệu, thống kê… Các vấn đề tính toán sẽ được xử lý nhanh hơn so với việc lập trình trên các ngôn ngữ như C, Java… dễ dàng tạo ra kết quả, vẽ đồ thị... Phần mềm này có thể được sử dụng cho xử lý tín hiệu, phân tích thống kê, xử lý ảnh, mô phỏng động lực chất lưu, và tối ưu hóa.
Cú pháp của Scilab tương tự như MATLAB, Scilab bao gồm bộ chuyển đổi mã nguồn từ MATLAB. Scilab hiện sẵn dùng miễn phí dưới giấy phép mã nguồn mở. Do tính chất đó một số đóng góp của người dùng đã được tích hợp vào Scilab.
* Phần mềm nhỏ gọn, tiện sử dụng, thích hợp cho việc giảng dạy. Scilab và Octave được đánh giá là 2 phần mềm mã nguồn mở gần với MatLab nhất.

Trang chủ: http://www.scilab.org/
Tài liệu hướng dẫn sử dụng:

• Hướng dẫn cho người mới
• Mô hình hóa các hiện tượng vật lý bằng Scilab
• Hướng dẫn Scilab cho học phần Toán cao cấp 

Xem thêm Dùng Scilab lập trình kiểm tra tính nguyên tố.


 

Read More

Cuộc đời đó có bao lâu mà hững hờ*

Người ta có thể đi rất nhiều nơi trên trái đất này, nhưng đi thế nào để tận hưởng cuộc sống và  lúc trở về còn có gì để nhớ  lại là một chuyện khác.

Tại sao bạn đi?

Tôi ít khi tham gia vào những đoàn phượt có quá 10 thành viên, phần vì như vậy sẽ làm loãng mối quan hệ, phần vì tôi không thích một chuyến đi quá ồn ào và náo nhiệt. Nhiều bạn trẻ thường đưa ra những lý do rất hay để khởi đầu cho chuyến đi của mình: đi vì “hạnh phúc là con đường”, đi để chinh phục những giới hạn của con người, đi là để thêm yêu quê hương đất nước, phượt để kết hợp các hoạt động thiện nguyện quyên góp cho trẻ em vùng cao…

 Còn tôi đi là để trốn tránh những mỏi mệt trong cuộc sống thường ngày của mình. Nghe thật chẳng có chút gì .. lý tưởng . Nhưng người ta có quyền gác lại hoạt động “cứu thế giới” sang một bên và sống ích kỷ cho riêng mình trong một vài ngày chứ?

Đọc tiếp »

Read More